Задача: Найти общее уравнение функции (в виде y = F(x))
Условия:
Есть область в диапазоне значений 0..256, 0..256.
На оси X между 0 и 256 задана точка M.
В этой области есть две ограничивающие прямые:
y = x
и
y = 256256 - M· x - 256 · M256 - M
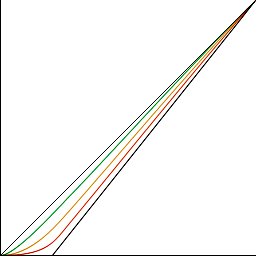
Между этими двумя прямыми возможно семейство гладких кривых, промежуточное положение которых зависит от параметра N. (Например, при N = 0 кривая совпадает с первой прямой, а при N = 256 кривая совпадает со второй прямой.)

Я пробовал подобрать кубическое уравнение (гиперболический сплайн) вида:
L = (256 / (256 - M)) * x - (256 / (256 - M)) + M - D +
√(E2 * 2562 - L2 + E2 * F * x2 - L2 * F * x2 / 2562) +
√(E2 * 2562 - L2 + E2 * 2562 * G * (256 + Off - x) - (256 + Off - x)2 / 2562 - L2 * G * (256 + Off - x) - (256 + Off - x)2 / 2562)
но это уравнение не параметризуется в N, и не дает достаточной крутизны при приближении к точке (0, M). Абсолютное совпадение кривой с точкой M возможно только в уравнении бесконечного порядка. Поскольку мне не нужно точного совпадения со второй прямой, я решил попробовать применить кривую Безье, которая, как мне кажется в данном случае, выражается уравнением шестого порядка.
Уравнение кривой Безье у меня есть только в параметрическом виде:
x = Pax(t3 + 3t2 - 3t + 1) + 3Pbxt(t2 - 2t + 1) + 3Pcxt2(1 - t) + Pdxt3
y = Pay(t3 + 3t2 - 3t + 1) + 3Pbyt(t2 - 2t + 1) + 3Pcyt2(1 - t) + Pdyt3
Для точек Pa, Pb, Pc и Pd с координатами
Pa: (0, 0)
Pb: (0, M)
Pc: (0, M)
Pd:(256, 256)
первый член можно отбросить, так как точка Pa имеет координаты (0, 0):
x = 3Pbxt(t2 - 2t + 1) + 3Pcxt2(1 - t) + Pdxt3
y = 3Pbyt(t2 - 2t + 1) + 3Pcyt2(1 - t) + Pdyt3
В этом примере для приближения я взял точки Pb и Pc совпадающими, но может оказаться, что что они не совпадают и в верхней части кривой есть излом (то есть, касательная к кривой в средних значениях (128, ?) не проходит через точку (256, 256), а имеет некий промежуточный угол наклона между углами наклонов первой и второй прямой)
В общем, точки Pb и Pc не обязаны совпадать, но для набора кривых без перегиба в верхней части эти точки совпадают.
Короче, я застрял на том, что не могу привести это дурацкое параметрическое уравнение к стандартному виду, даже не говоря о том, чтобы написать зависимость этого уравнения от N [0..256].
Мне нужно:
Примечание:
Подбираемая функция - это передаточная функция яркости изображения в пространстве RGB. Смысл ее в том, что в диапазоне средних значений яркости [T1..T2], причем неизвестно заранее каком, эта функция похожа на прямую. На краях функции [0..T1] и [T2..255] функция плавно сглаживается к точкам (0, 0) и (256, 256) соответственно. При N равном 0 кривая всегда совпадает с прямой y = x. При N равном 256 кривая стремится к прямой, проходящей через точку M. Если пытаться использовать кривую Безье, то для этой кривой в общем случае надо даже 5 точек, а не 4, но упрощение из четырех точек тоже может подойти, хотя в этом случае координаты точки Pc не всегда просто выразить через входной параметр N. Физически эта функция осуществляет вычитание маски M с множителем n из изображения X. То есть, производит преобразование изображения Y = X - nM.
В самом сокращеном виде вопрос звучит так:
Какой должна быть подстановка для приведения уравнения вида
x = At3 + Bt2 + Ct
к виду t = F(x)?
Или:
Как привести систему параметрических уравнений
x = At3 + Bt2 + Ct
y = Dt3 + Et2 + Ft
к виду y = F(x)?
Полное уравнение
| Точки | Параметры |
| A | (A, E) |
| B | (B, F) |
| C | (C, G) |
| D | (D, H) |
x = A (t^3 + 3 t^2 - 3 t + 1) + B t (t^2 - 2 t + 1) + C t^2 (1 - t) + D t^3 y = E (t^3 + 3 t^2 - 3 t + 1) + F t (t^2 - 2 t + 1) + G t^2 (1 - t) + H t^3
x = A t^3 + 3 A t^2 - 3 A t + A + B t^3 - 2 B t^2 + B t + C t^2 - C t^3 + D t^3 y = E t^3 + 3 E t^2 - 3 E t + E + F t^3 - 2 F t^2 + F t + G t^2 - G t^3 + H t^3
x = A t^3 + B t^3 - C t^3 + D t^3 + 3 A t^2 - 2 B t^2 + C t^2 + B t - 3 A t + A y = E t^3 + F t^3 - G t^3 + H t^3 + 3 E t^2 - 2 F t^2 + G t^2 + F t - 3 E t + E
x = (A + B - C + D) t^3 + (3 A - 2 B + C) t^2 + (B - 3 A) t + A y = (E + F - G + H) t^3 + (3 E - 2 F + G) t^2 + (F - 3 E) t + E
x -> E
t -> x
(A + B - C + D) x^3 + (3 A - 2 B + C) x^2 + (B - 3 A) x + A - E = 0
Для фиксированной точки A (0, 0)
t = (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * B - 3 * C + D)) - (2^(1/3) * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)) / (3 * (3 * B - 3 * C + D) * (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3)) + (2 * B - C) / (3 * B - 3 * C + D)
Для фиксированной точки A (0, 0) и скомбинированных точек B и C
t = -(-2 * C^3 * D^6 + 3 * C^2 * D^7 + (-3 * C^4 * D^14 + 4 * C^3 * D^15 + 4 * C^3 * D^14 * x - 6 * C^2 * D^15 * x + D^16 * x^2)^(1/2) + D^8 * (-x))^(1/3) / (2^(1/3) * D^3) + (2^(1/3) * (9 * C * D^5 - 9 * C^2 * D^4)) / (9 * D^3 * (-2 * C^3 * D^6 + 3 * C^2 * D^7 + (-3 * C^4 * D^14 + 4 * C^3 * D^15 + 4 * C^3 * D^14 * x - 6 * C^2 * D^15 * x + D^16 * x^2)^(1/2) + D^8 * (-x))^(1/3)) + C / D
Полное уравнение для фиксированной точки A (0, 0)
y = 3 * F * t * (t^2 - 2 * t + 1) + 3 * G * t^2 * (1 - t) + H * t^3
y = (3 * F - 3 * G + H) * (t)^3 + (3 * G - 6 * F) * (t)^2 + 3 * F * (t)
y = (3 * F - 3 * G + H) * ((-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * B - 3 * C + D)) - (2^(1/3) * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)) / (3 * (3 * B - 3 * C + D) * (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3)) + (2 * B - C) / (3 * B - 3 * C + D))^3 + (3 * G - 6 * F) * ((-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * B - 3 * C + D)) - (2^(1/3) * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)) / (3 * (3 * B - 3 * C + D) * (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3)) + (2 * B - C) / (3 * B - 3 * C + D))^2 + 3 * F * ((-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * B - 3 * C + D)) - (2^(1/3) * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)) / (3 * (3 * B - 3 * C + D) * (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * C + 9 * B * D - 9 * C^2)^3 + (-54 * B^3 + 81 * B^2 * C - 162 * B^2 * D + 243 * B^2 * x + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^2)^(1/2) + 81 * B * C^2 + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C^3 + 243 * C^2 * x - 162 * C * D * x + 27 * D^2 * x)^(1/3)) + (2 * B - C) / (3 * B - 3 * C + D))
Полное уравнение для фиксированной точки A (0, 0) и скомбинированных точек B и C (F = G)
y = 3 * G * t * (t^2 - 2 * t + 1) + 3 * G * t^2 * (1 - t) + H * t^3
y = H * (t)^3 - 3 * G * (t) ^2 + 3 * G * (t)
Javascript
t = Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3) / (3 * Math.pow(2, 1/3) * (3 * B - 3 * C + D)) - (Math.pow(2, 1/3) * (-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C)) / (3 * (3 * B - 3 * C + D) * Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3)) + (2 * B - C) / (3 * B - 3 * C + D)
Для фиксированной точки A (0, 0) и скомбинированных точек B и C
t = -Math.pow(-2 * C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3) / (Math.pow(2, 1/3) * D * D * D) + (Math.pow(2,
1/3) * (9 * C * D * D * D * D * D - 9 * C * C * D * D * D * D)) / (9 * D * D * D * Math.pow(-2 * C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3)) + C / D
Полное уравнение для фиксированной точки A (0, 0)
y = (3 * F - 3 * G + H) * Math.pow(t, 3) + (3 * G - 6 * F) * Math.pow(t, 2) + 3 * F * (t);
y = (3 * F - 3 * G + H) * Math.pow(Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3) / (3 * Math.pow(2, 1/3) * (3 * B - 3 * C + D)) - (Math.pow(2, 1/3) * (-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C)) / (3 * (3 * B - 3 * C + D) * Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3)) + (2 * B - C) / (3 * B - 3 * C + D), 3) + (3 * G - 6 * F) * Math.pow(Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3) / (3 * Math.pow(2, 1/3) * (3 * B - 3 * C + D)) - (Math.pow(2, 1/3) * (-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C)) / (3 * (3 * B - 3 * C + D) * Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3)) + (2 * B - C) / (3 * B - 3 * C + D), 2) + 3 * F * (Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3) / (3 * Math.pow(2, 1/3) * (3 * B - 3 * C + D)) - (Math.pow(2, 1/3) * (-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C)) / (3 * (3 * B - 3 * C + D) * Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + Math.pow(4 * Math.pow(-9 * B * B + 9 * B * C + 9 * B * D - 9 * C * C, 3) + Math.pow(-54 * B * B * B + 81 * B * B * C - 162 * B * B * D + 243 * B * B * x + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 2), 0.5) + 81 * B * C * C + 81 * B * C * D - 486 * B * C * x + 162 * B * D * x - 54 * C * C * C + 243 * C * C * x - 162 * C * D * x + 27 * D * D * x, 1/3)) + (2 * B - C) / (3 * B - 3 * C + D));
Полное уравнение для фиксированной точки A (0, 0) и скомбинированных точек B и C (F = G)
y = H * Math.pow(t, 3) - 3 * G * Math.pow(t, 2) + 3 * G * (t);
y = H * Math.pow(-Math.pow(-2 * C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3) / (Math.pow(2, 1/3) * D * D * D) + (Math.pow(2,
1/3) * (9 * C * D * D * D * D * D - 9 * C * C * D * D * D * D)) / (9 * D * D * D * Math.pow(-2 * C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3)) + C / D, 3) - 3 * G * Math.pow(-Math.pow(-2
* C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3) / (Math.pow(2, 1/3) * D * D * D) + (Math.pow(2,
1/3) * (9 * C * D * D * D * D * D - 9 * C * C * D * D * D * D)) / (9 * D * D * D * Math.pow(-2 * C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3)) + C / D, 2) + 3 * G * (-Math.pow(-2
* C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3) / (Math.pow(2, 1/3) * D * D * D) + (Math.pow(2,
1/3) * (9 * C * D * D * D * D * D - 9 * C * C * D * D * D * D)) / (9 * D * D * D * Math.pow(-2 * C * C * C * D * D * D * D * D * D + 3 * C * C * D * D * D * D * D * D * D +
Math.pow(-3 * C * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D + 4 * C * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x - 6 * C * C * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x + D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * D * x * x, 0.5) + D * D * D * D * D * D * D * D * (-x), 1/3)) + C / D);
AviSintth
(3 F - 3 G + H) ((-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + (4 (-9 B^2 + 9 B C + 9 B D - 9 C^2)^3 + (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^2)^(1/2) + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^(1/3) / (3 2^(1/3) (3 B - 3 C + D)) - (2^(1/3) (-9 B^2 + 9 B C + 9 B D - 9 C^2)) / (3 (3 B - 3 C + D) (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + (4 (-9 B^2 + 9 B C + 9 B D - 9 C^2)^3 + (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^2)^(1/2) + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^(1/3)) + (2 B - C) / (3 B - 3 C + D))^3 + (3 G - 6 F) ((-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + (4 (-9 B^2 + 9 B C + 9 B D - 9 C^2)^3 + (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^2)^(1/2) + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^(1/3) / (3 2^(1/3) (3 B - 3 C + D)) - (2^(1/3) (-9 B^2 + 9 B C + 9 B D - 9 C^2)) / (3 (3 B - 3 C + D) (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + (4 (-9 B^2 + 9 B C + 9 B D - 9 C^2)^3 + (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^2)^(1/2) + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^(1/3)) + (2 B - C) / (3 B - 3 C + D))^2 + 3 F ((-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + (4 (-9 B^2 + 9 B C + 9 B D - 9 C^2)^3 + (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^2)^(1/2) + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^(1/3) / (3 2^(1/3) (3 B - 3 C + D)) - (2^(1/3) (-9 B^2 + 9 B C + 9 B D - 9 C^2)) / (3 (3 B - 3 C + D) (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + (4 (-9 B^2 + 9 B C + 9 B D - 9 C^2)^3 + (-54 B^3 + 81 B^2 C - 162 B^2 D + 243 B^2 x + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^2)^(1/2) + 81 B C^2 + 81 B C D - 486 B C x + 162 B D x - 54 C^3 + 243 C^2 x - 162 C D x + 27 D^2 x)^(1/3)) + (2 B - C) / (3 B - 3 C + D))
Полное уравнение для фиксированной точки A (0, 0)
BEZIER = "(3 * " + string(F) + " - 3 * " + string(G) + " + " + string(H) + ") * ((-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + (4 * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + ")) - (2^(1/3) * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)) / (3 * (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + ") * (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + (4 * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * " + string(B) + " - " + string(C) + ") / (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + "))^3 + (3 * " + string(G) + " - 6 * " + string(F) + ") * ((-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + (4 * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + ")) - (2^(1/3) * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)) / (3 * (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + ") * (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + (4 * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * " + string(B) + " - " + string(C) + ") / (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + "))^2 + 3 * " + string(F) + " * ((-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + (4 * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + ")) - (2^(1/3) * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)) / (3 * (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + ") * (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + (4 * (-9 * " + string(B) + "^2 + 9 * " + string(B) + " * " + string(C) + " + 9 * " + string(B) + " * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * " + string(B) + "^3 + 81 * " + string(B) + "^2 * " + string(C) + " - 162 * " + string(B) + "^2 * " + string(D) + " + 243 * " + string(B) + "^2 * x + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * " + string(B) + " * " + string(C) + "^2 + 81 * " + string(B) + " * " + string(C) + " * " + string(D) + " - 486 * " + string(B) + " * " + string(C) + " * x + 162 * " + string(B) + " * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * " + string(B) + " - " + string(C) + ") / (3 * " + string(B) + " - 3 * " + string(C) + " + " + string(D) + "))"
Полное параметризированное на высветление уравнение для фиксированной точки A (0, 0)
| MaxX | Density | y | |
| 20 | 256 | 52 | 20 |
| 20 | 256 | 0 | 0 |
| 20 | 0 | 52 | 0 |
| 20 | 0 | 0 | 0 |
| 20 | 128 | 52 | 10 |
| 20 | 0 | 52 | 0 |
| 20 | 64 | 52 | 5 |
| 20 | 128 | 52 | 10 |
| 20 | 192 | 52 | 15 |
| 20 | 256 | 52 | 20 |
| 20 | 192 | 26 | 7.5 |
z = 13312 = 52 * 256 = MaskMax * Space
B = MaxX * Density * y / (MaskMax * Space)
MaskMax = 52
MaxX = 90
MaxY = 20
ZX = MaskMax * Space / MaxX # 147,9
ZY = MaskMax * Space / MaxY # 665,6
B: Density * y / ZX
G: Density * y / ZY
| " + string(B) + " | (" + string(Density) + " * y / " + string(ZX) + ") |
| " + string(G) + " | (" + string(Density) + " * y / " + string(ZY) + ") |
BEZIER = "(3 * " + string(F) + " - 3 * (" + string(Density) + " * y / " + string(ZY) + ") + " + string(H) + ") * ((-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + ")) - (2^(1/3) * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)) / (3 * (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + ") * (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * (" + string(Density) + " * y / " + string(ZX) + ") - " + string(C) + ") / (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + "))^3 + (3 * (" + string(Density) + " * y / " + string(ZY) + ") - 6 * " + string(F) + ") * ((-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + ")) - (2^(1/3) * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)) / (3 * (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + ") * (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * (" + string(Density) + " * y / " + string(ZX) + ") - " + string(C) + ") / (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + "))^2 + 3 * " + string(F) + " * ((-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + ")) - (2^(1/3) * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)) / (3 * (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + ") * (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " - 9 * " + string(C) + "^2)^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 + 81 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(C) + " - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + "^2 + 81 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * " + string(D) + " - 486 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(C) + " * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x - 54 * " + string(C) + "^3 + 243 * " + string(C) + "^2 * x - 162 * " + string(C) + " * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * (" + string(Density) + " * y / " + string(ZX) + ") - " + string(C) + ") / (3 * (" + string(Density) + " * y / " + string(ZX) + ") - 3 * " + string(C) + " + " + string(D) + "))"
Нуль сбалансированнное уравнение для фиксированной точки A (0, 0) и фиксированной точки С (0, 0)
С (0, 0)
B (0 - Mask)
A = 0
E = 0
B [0..M]
F = 0
C = 0
G = 0
D = Max
H = Max
y = H * ((-54 * B^3 - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * D)^3 + (-54 * B^3 - 162 * B^2 * D + 243 * B^2 * x + 162 * B * D * x + 27 * D^2 * x)^2)^(1/2) + 162 * B * D * x + 27 * D^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * B + D)) - (2^(1/3) * (-9 * B^2 + 9 * B * D)) / (3 * (3 * B + D) * (-54 * B^3 - 162 * B^2 * D + 243 * B^2 * x + (4 * (-9 * B^2 + 9 * B * D)^3 + (-54 * B^3 - 162 * B^2 * D + 243 * B^2 * x + 162 * B * D * x + 27 * D^2 * x)^2)^(1/2) + 162 * B * D * x + 27 * D^2 * x)^(1/3)) + (2 * B) / (3 * B + D))^3
| B | (" + string(Density) + " * y / " + string(ZX) + ") |
| D | " + string(D) + " |
| H | " + string(H) + " |
BEZIER = "" + string(H) + " * ((-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + ")^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3) / (3 * 2^(1/3) * (3 * (" + string(Density) + " * y / " + string(ZX) + ") + " + string(D) + ")) - (2^(1/3) * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + ")) / (3 * (3 * (" + string(Density) + " * y / " + string(ZX) + ") + " + string(D) + ") * (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + (4 * (-9 * (" + string(Density) + " * y / " + string(ZX) + ")^2 + 9 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + ")^3 + (-54 * (" + string(Density) + " * y / " + string(ZX) + ")^3 - 162 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * " + string(D) + " + 243 * (" + string(Density) + " * y / " + string(ZX) + ")^2 * x + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^2)^(1/2) + 162 * (" + string(Density) + " * y / " + string(ZX) + ") * " + string(D) + " * x + 27 * " + string(D) + "^2 * x)^(1/3)) + (2 * (" + string(Density) + " * y / " + string(ZX) + ")) / (3 * (" + string(Density) + " * y / " + string(ZX) + ") + " + string(D) + "))^3"
MaxY = 0
B = MaxX * Density * y / (MaskMax * Space)
MaskMax = 52
MaxX = 90
MaxY = 20
ZX = MaskMax * Space / MaxX # 147,9
ZY = MaskMax * Space / MaxY # 665,6
B: Density * y / ZX
G: Density * y / ZY